Coneixem 3 igualtats notables, cadascuna amb la seva regla:
-(a+b)2= a2 +2ab+b2
-(a-b)2=a2-2ab+b2
-(a+b)(a-b)=a2+b2
A continuació posarem alguns exemples:
-(3x+8)2= (3x)2+2·8+82=9x2+48x+64


Triangle

Trapezi
Volums
Volum d'un cilindre:
Volum d'una esfera:
-(6x4-5x)=(6x4)2-2·6x4·5x+5x2=368-60x5+25x2
-(2x-7)(2x+7)=(2x)2-72=4x2-49
Un truc per seber si hem fet bé una operació d'igualtats notables, és que si mierem els exponents de cada numero/incógnita i veiem quan es porten, es a dir. Si un exponent es per exemple 4 i un altre és 2 vol dir que es porten dos. Per tant en el resultat de l'operació els exponents han de anar de dos en dos.
Exemple:
Com podem apreciar veiem que, 8,6 i 4 van de dos en dos.
Aquí os deixo un link:
http://www.vitutor.com/ab/p/i_e.html
Sistema d'equacions
Exemple:
2x+y=5
3x-2y=11
y=5-2x
3x-2y=11
3x-2(5-2x)=11
3x-10+4x=11
7x=11+10
7x=21
x=21/7
x=3
y=5-2x
y=5-2·3
y=5-6
y=-1
Probleames de sistemes
Aquí he posat un problema resolt perquè pugueu veure com es fa, a continuació us deixo un link amb tot de problemes de sistemes amb les seves solucions:
http://www.vitutor.com/ecuaciones/sistemas/problemas_%E2%80%8Bsistemas.html
Teorema de Tales
Primer per entendre-ho millor podeu veure aquest video:
Doncs molt com hem vist l'únic que tenim que fer és aplicar la regla de 3.
Exercicis:
http://www.vitutor.com/geo/eso/ss_1e.html
Àrees
Primer us ensenyaré a fer Pitàgores, és mol fácil.
-(6x4+3x2)=(6x4)2+2·6x4·3x2+(3x2)2=36x8+36x6+9x4
Com podem apreciar veiem que, 8,6 i 4 van de dos en dos.
Aquí os deixo un link:
http://www.vitutor.com/ab/p/i_e.html
Sistema d'equacions
Els sistemes d'equacions són un conjunt d'equcions, però de moment sol coneixem la de dos incognites. Les resolem amb el mode de substitució. (per saber millor de quina equació parlem els hi posarem equació 1 i equació 2)Tracta de aillar una incógnita x en la equació 1 i subsituir el que has aillat per la mateixa incognita x de la equació 2. Resolem la equació 2 i deprés donará l'altra incógnita y. Ara canviarem la incognita y de l'atre equació 1 per la que ens ha donat l'equació 2. Resolem i trobem la incógnita x.
Exemple:
2x+y=5
3x-2y=11
y=5-2x
3x-2y=11
3x-2(5-2x)=11
3x-10+4x=11
7x=11+10
7x=21
x=21/7
x=3
y=5-2x
y=5-2·3
y=5-6
y=-1
Probleames de sistemes
Una granja tiene pavos y cerdos, en total hay 58 cabezas y 168
patas. ¿Cuántos cerdos y pavos hay?
x :número de pavos.
y :número de cerdos.
x+y=58
2x+4y=168
-2x-2y=-116
2x+4y=168
2y=52
y=26
x+26=58
x=32
32 :número
de pavos.
26 :número
de cerdos.
Aquí he posat un problema resolt perquè pugueu veure com es fa, a continuació us deixo un link amb tot de problemes de sistemes amb les seves solucions:
http://www.vitutor.com/ecuaciones/sistemas/problemas_%E2%80%8Bsistemas.html
Teorema de Tales
Primer per entendre-ho millor podeu veure aquest video:
Doncs molt com hem vist l'únic que tenim que fer és aplicar la regla de 3.
Sabem que l'arbre mesura 5 metres i la seva ombra 6 metres. L'altutura del edifici no la sabem, li direm x i la seva ombra fa 270 metres per tant:
x/260=5/6
x/260=5/6
6x=270·5
6x=1350
X=1350/6
X=225Exercicis:
http://www.vitutor.com/geo/eso/ss_1e.html
Àrees
Primer us ensenyaré a fer Pitàgores, és mol fácil.
a2=b2+c2
Exemple:
x2=32+62
x2=9+36
x2=45
x=arrel quadrada de 45
x=6,70
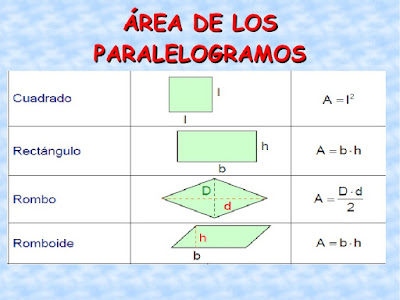
Àrea dels paral·lelograms:
Àrea del triangle i del trapezi


Triangle

Trapezi
Àrea d'un polígon regular
Exercicis:
Volums
Volum d'un prisma:
V=Àrea de la base· altura
52=a2+2,52
25=a2+6,25
a2=25-6,25
a2=18,75
a=arrel quadrada de 18,75
a=4,33 cm2
Àrea de la base=
30·4,33=129,9/2=64,95
Volum:
64,95·10=649,5 cm3
Volum d'una piràmide:
Volum d'un cilindre:
Àrea de la base per altura
Volum d'un con:
Volum d'una esfera:














No hay comentarios:
Publicar un comentario